holomorphe

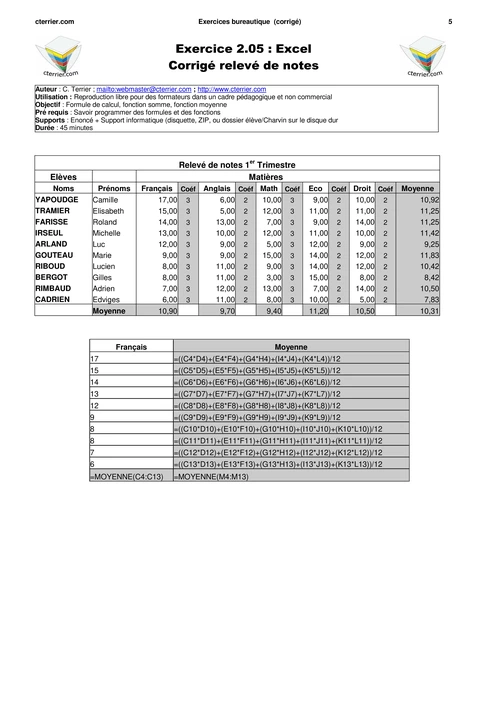Université de Rennes 1. Calcul différentiel et fonctions holomorphes. Année
2008-2009. Contrôle continu no2-Corrigé. Exercice 1. On pose z = x + iy, avec x,y
 ...

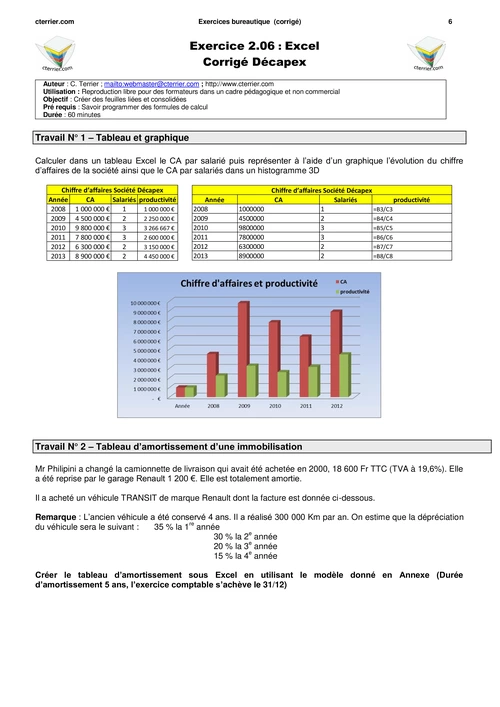Fonctions holomorphes - Corrigé. Exercice 2.1. ... partielles sont continues) pour
affirmer que f est holomorphe. Exercice .... seul intervalle (cf dessin fait en TD).

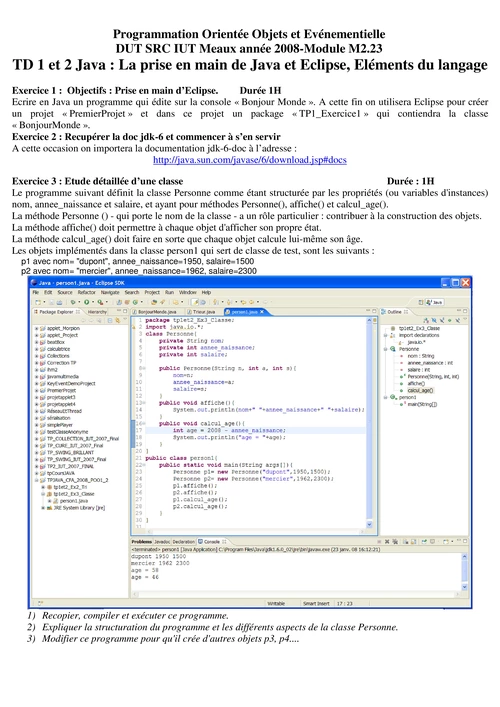Université Pierre et Marie Curie. Licence de Mathématiques L3. LM367. 2011-
2012. Corrigé partiel de l'interro 1. Exercice 1. Soit f une fonction holomorphe ...

2012-2013 : TD 6. Convergence de suites de fonctions holomorphes. M. Triestino
, A. Vaugon. Corrigé. Exercice 1. (Théorème de Hurwitz) Soit ? ? C ouvert ...

Exercices - Topologie et fonctions holomorphes : corrigé. Déterminations.
Exercice 1 - Racine carrée - L3/M1 - ?. Pour qu'une fonction holomorphe f : ? ?
C? ...

Exercices - Singularités des fonctions holomorphes - fonctions méromorphes :
corrigé. Exercice 1 - Domaine de convergence - L3/M1 - ?. On décompose la ...

L5 - Fonctions holomorphes. Corrigé de l'examen du 22 Juin 2009. Exercice 1. 1,
a. D'après les formules de Cauchy, on a an = 1. 2?i ?? f(?) ?n+1 d? pour n ? 0,.

Exercice 1.2.9 On va simplement corriger la deuxième question, la première en ...
vertes, i.e l'image d'un ouvert par une fonction holomorphe non constante est ...

Examen du 12 janvier 2005 ? durée : 3 heures. Corrigé. 1. Soit U = {1 < |z| < 2} et
soit f : U ? C une fonction holomorphe. On note u = Re(f) et v = Im(f). 1.1.

Déterminer l'ensemble des fonctions f holomorphes sur C dont la partie réelle P
est: ... Soit ?, un ouvert connexe de C, et f, une fonction holomorphe sur ?. 1.